String Theory
Using
and Abusing the
Rick
Kemper,
Brook Taylor
1685-1731
Remembered
primarily for his work in Mathematics and Physics, Brook Taylor was also an
accomplished artist and musician. Brook
Taylor’s work propelled the budding science of differential
calculus. Physicists admired his papers
on capillary action, magnetism and thermometers. His experiments with strings helped unite
the arts of music and luthiery with the practical applied mathematics and
physics. His equation gave physicists
and instrument builders a way to accurately predict the fundamental behavior of
a plucked string;
T= M (2L F)2
Where
T is the tension
of the string
M is the linear
mass
F is the
Frequency
L is the Length
of the string
Let us take a
fairly simple case, the 440 Hz A just above middle C. On most nylon strung harps, this will be
about .045” in diameter, about 16 inches long. Nylon has a density of .0385 lbs/cubic
inch. The
First calculate
the linear mass,
M.045 = Cross Sectional Area x 
= 
(.045in/2)2 
= 1.599 x 10-7
Then use that to
calculate the tension on the string
T = M
(2L F)2 = 1.599 x 10-7 (2 x 16 inches x 440 Hz)2= 31.4 lbs
Now string
makers use this equation to calculate the total tension on the harp, and it
works well for that. The
To illustrate
this, let us take the example an Italian Lute builder, Giuseppe. Our Guiseppe, he
wants to make an instrument with a 523 Hz C string. Can
We can now
rearrange the terms of
M.040 =
(.040in/2)2 = 1.253 x 10-7
T.040max= Breaking Strength x Area = 44,600 lbs /in2 x (.040in/2)2 = 56 lbs
Now we can use
L.040max = 
= 
= 20.2 inches
An interesting
thing happens when we decide to calculate the maximum breaking length for .025 nylon;
L.025max = = 
= 20.2 inches
In fact, for any
monofilament 523 Hz C string
L.025max = L.028max = L.032max = L.036max = L.040max = L.045max =20.2 inches = Lmax
for any nylon string!
The breaking
length is independent of he string’s gauge!
Orchestral Pedal
harps place a premium on volume – the harp needs to be heard over a
hundred other instruments. A designer
makes these harps louder by using large soundboards, heavy gauge strings, and
string lengths that are near the maximum.
Playing these harps at volume requires a forceful technique and it is no
surprise that many professional players develop stress injuries at some point in
their playing career.
Now, few harp
builders are willing to put up with string lengths that are right at the design
limit – the harp will just break too many strings. Most designers will use a margin of safety
and set an arbitrary limit, usually 65-95% of the string’s breaking
strength. Using the
|
Note |
Pitch (Hz) |
Max Length (inches) |
|
C7 |
2093 |
4.9 |
|
B6 |
1976 |
5.2 |
|
A6 |
1760 |
5.9 |
|
G6 |
1568 |
6.6 |
|
F6 |
1397 |
7.4 |
|
E6 |
1319 |
7.8 |
|
D6 |
1175 |
8.8 |
|
C6 |
1047 |
9.8 |
|
B5 |
988 |
10.4 |
|
etc. |
|
|
The lower limit
for string length is not as distinct.
Most designers will set an arbitrary limit where the string “feels
to floppy” to sound effectively.
Some place this limit at 40% of the breaking strength; others are
willing to bend the rules, especially at the bass end to 15% of the breaking
strength. If we arbitrarily set that
lower limit at 30% we can generate a useful table that calculates the
theoretical upper and lower limits for monofilament string lengths:
|
Note |
Pitch |
30% Min |
95% Max |
|
Note |
Pitch |
30% Min |
95% Max |
|
C7 |
2093 |
2.8 |
4.9 |
|
F4 |
349 |
16.6 |
29.5 |
|
B6 |
1976 |
2.9 |
5.2 |
|
E4 |
330 |
17.6 |
31.3 |
|
A6 |
1760 |
3.3 |
5.9 |
|
D4 |
294 |
19.7 |
35.1 |
|
G6 |
1568 |
3.7 |
6.6 |
|
C-m |
262 |
22.1 |
39.4 |
|
F6 |
1397 |
4.1 |
7.4 |
|
B3 |
247 |
23.5 |
41.7 |
|
E6 |
1319 |
4.4 |
7.8 |
|
A3 |
220 |
26.3 |
46.8 |
|
D6 |
1175 |
4.9 |
8.8 |
|
G3 |
196 |
29.5 |
52.6 |
|
C6 |
1047 |
5.5 |
9.8 |
|
F3 |
175 |
33.2 |
59.0 |
|
B5 |
988 |
5.9 |
10.4 |
|
E3 |
165 |
35.1 |
62.5 |
|
A5 |
880 |
6.6 |
11.7 |
|
D3 |
147 |
39.4 |
70.2 |
|
G5 |
784 |
7.4 |
13.1 |
|
C3 |
131 |
44.3 |
78.8 |
|
F5 |
698 |
8.3 |
14.8 |
|
B2 |
123 |
46.9 |
83.5 |
|
E5 |
659 |
8.8 |
15.6 |
|
A2 |
110 |
52.6 |
93.7 |
|
D5 |
587 |
9.9 |
17.5 |
|
G2 |
98 |
59.1 |
105.2 |
|
C5 |
523 |
11.1 |
19.7 |
|
F2 |
87 |
66.3 |
118.0 |
|
B4 |
494 |
11.7 |
20.9 |
|
E2 |
82 |
70.3 |
125.1 |
|
A4 |
440 |
13.2 |
23.4 |
|
D2 |
73 |
78.9 |
140.4 |
|
G4 |
392 |
14.8 |
26.3 |
|
C2 |
65 |
88.5 |
157.6 |
Graphed out,
they look like this:
Some
observations – Bass string lengths greater than 60 or 70 inches are
problematic for two reasons. The harp is
unreasonably LARGE (to transport) and the amplitude of the plucked string will
require greater spacing to keep it from hitting the adjacent strings or the
harpists fingers as she reaches in to pluck an adjacent string. Spacing greater than 5” per octave or
so reduces the player’s ability to play useful intervals like octaves and
tenths with the left hand. Because of
these considerations, most designs greater that three or four octaves will
employ wound bass strings. Wound bass
strings can be made in a variety of configurations. The bottom notes of five and six octave harps
employ a steel core over-wrapped with bronze or copper wire. Most strings with a metal core use fiber
bedding between the core and wrap. The core carries the tension, and the over
wrap can dramatically increase the string’s linear mass, allowing a
relatively short string to achieve big fat bass notes.
The trick is to
come up with a string band that transitions gracefully
from monofilament to wound strings without any abrupt changes in string’s
tone, length or feel.
The
%TS or TEN% is short for Percentage of
the tensile strength. This parameter
gives the string’s tension as a percentage of its breaking strength. Let us calculate the tension on the 523hz C on a L&H Troubadour. The vibrating length is 14.4 inches. It is usually .040 or .045 gauge nylon. Let say it is .040 nylon. We can use the
T= M (2L F)2 =
1.253E-07 (2 (14.4in)523Hz)2 = 28.4 lbs Tension
The breaking
strength of .040 nylon was calculated earlier at 56.0
lbs, so
%TEN = 28.4/56.0 =.507 or 50.7%
It is important
to note that the
T/L is called the Tension to
length ratio and is the strings Tension divided by the length. Using the same string referenced above,
T/L = 28.4 lbs/14.4inches = 1.97
By itself, for
an individual string, T/L is not a very useful number. The idea is that longer strings should have
more tension. If they did not, they
would feel floppy relative to shorter strings with the same tension. Harpists seem to feel most comfortable with
string bands that start with a T/L ratio around 3-6 (Using the English units
measurement of lb/in), typically descending to about .8 – 1.0 in the
fifth octave. When they develop a
string table, makers will usually scan down the T/L column looking for any
sudden changes.
There are three
good reasons for bass strings to have greater tension than the treble
strings. Most music requires longer
ringing chords in the bass end. To get
that sustain, you need to take the initial energy (the pluck) and distribute it
over time. Second, Higher tension limits
the amplitude of the plucked strings which allows them to be spaced reasonably
close. Lastly, bass notes need a
significant amount of energy to be heard as well as higher notes. The speakers that make the bass notes are
big and their cones are heavy (relative to a tweeter).
Now, let’s take a look
at some harp string bands to see how the TEN% and T/L vary among different
designs. I will start with a vintage
Witcher design, a 32 string harp similar to the one shown on the Sylvia Woods
book, Teach Yourself to Play the Folk
Harp. With a ruler and micrometer, I
can measure the harps’ string lengths and gauges. The owner readily admitted that these are not
the original gauges, and that the harp had been restrung several times. Using the physical properties of the nylon
and
Tension; The thinner gauge strings
at the treble end only have 12 lbs on tension on them. The tension climbs fairly evenly up to 43 lbs
at the bass end. All together there is
about 840 lbs of tension on the harp.
Percent
Breaking Strength; %TEN starts near 60% of the breaking strength, and descends in to
about 30% at the last monofilament string, #22.
It jumps up back up to 54% for the first Nylon/Nylon wound string, and
then descends again to about 40%. All but one of the strings fall in between that 30-60% range. It is a pretty good medium tension design.
Tension to
Length Ratio;
The T/L ratio starts at 3.3 and descends fairly evenly in to 1.1 at the bass
end. There are no big jumps in the T/L
that would result in an uneven feel.
Now, let us take
a look at three other models. What can
these charts do to help us understand string band design?
The Music
Maker’s Gothic 31 (Monofillament Strings):
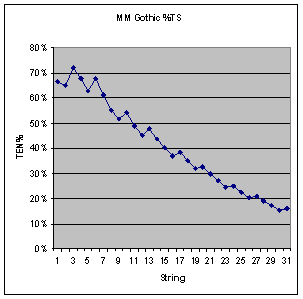
Looking at the
tension chart, one notes that the bass strings do not have as a high a tension as
the Witcher. All together, they total
about 640 lbs. This makes sense for kit
harp, where inexperienced builders may not be able to produce a super strong
frame with limited tools and clampage.
The long bass strings give it a very low %TS (descending down to 15%)
and T/L, (0.4). The bass strings that
are quite loose. Music Makers offers
an alternate set of wound strings that bring up the %TS and T/L considerably in
that last octave.
Triplett Axline
Like the Witcher, the string set I found
on this well-used Axline was probably not factory. I believe Triplett and Dusty both use bronze
core strings in the bass, and these were steel core. There is a small jump in the total percent
breaking strength (%TS) at the transition to wound nylon core nylon wrap
strings, but it is not as dramatic as it was in the Witcher. The tension to length ratio drops evenly
staying just above 1.0 at the bass end.
Fisher Eireann
The Eireann has been a real hit with hard
core Celtic Traditionalists. The finely
gauged incremental sizes of the Savarez monofilament strings yield some very
smooth lines. Without any the
nylon/nylon transition strings, the Tension, %TS and T/L all show a significant
“jump” at that transition from monofilament to Steel core bronze
wrap bass strings. When I play a
descending scale on the harp, I can certainly hear that change, but this
transition does not seem to bother many players.
Despite many these differences, there are
some interesting similarities among the four harps,
Tension starts at 10-20 lbs, and tends to
climb higher, reaching a maximum of 35-50 lbs in all four designs
%TS starts high and tends to go lower
staying between an upper bound of 70% at the treble end and 15-20% at the bass
end
T/L Starts around 3 and drops to about
1. The Music Makers harp is an
exception, falling to 0.4.
These are “rules of
thumb”. There are some very good
sounding designs that push or break these limits. Some harp designers take these rules of thumb
and attempt to translate them into equations that they claim will allow them to
calculate the
“optimal” string gauge or length for the “perfect”
instrument. I think this is folly.
After carefully measuring the strings on 60 harps and noting the
diversity among the best sounding ones, I can confidently state there is not a single optimal solution. Selecting the best string lengths and
gauges will depend on several other parameters, including but not limited to:
·
The soundboard materials used
·
The strength and technique of the player
·
How loud the harp needs to be
·
The builder’s ability to fabricate sound boxes, boards and
neck/pillar assemblies
I would be remiss if I did not to not
provide a table outlining the properties of various stringing materials. You can use these with the
Physical Properties of String Materials
|
|
Density (lb/in3) |
Density (kg/m3) |
Tensile Strength (lb/in2) |
Tensile Strength (kg/cm2) |
|
Tynex |
.0385 |
1,067 |
44,600 |
3,136 |
|
Synthetic Silk |
.0412 |
1,140 |
52,000 |
3,656 |
|
Gut |
.0469 |
1,300 |
52,000 |
3,656 |
|
Steel music wire |
.2829 |
7,830 |
325,000 |
2,2850 |
|
Bronze |
.3204 |
8,870 |
125,000 |
8,788 |
|
Brass |
.3048 |
8,437 |
110,000 |
7,734 |
|
Copper |
.3226 |
8,930 |
6,1000 |
4,289 |
Sourced from;
Joseph Jourdain’s The Folk Harp Stringband, fortepiano.com
Occasionally, some
well meaning nut will want to change the string material with which the harp is
strung. Nylon, Gut and Fluorocarbon have
densities and strengths that are close enough to be interchangeable provided
one selects gauges that do not increase the overall tension of the harp. What if a player wants to substitute metal
strings for nylon?
Cautious
technicians will sternly warn that substituting different string materials will
void any warranty for the harp. Often
the levers do not work. If the harp
owner persists in their wishes, can we use Mr. Brook Taylor’s equation to
discourage them farther?
Using the Physical Properties of String Materials, let’s generate a table
of monofilament string lengths for likely pitches so that the string will be at
30% and 70% of its theoretical breaking strength for brass, nylon and steel
strings.
|
|
|
Brass |
Nylon |
Steel |
|||
|
|
|
30% |
70% |
30% |
70% |
30% |
70% |
|
Note |
F (Hz) |
BL30 |
BL70 |
NL30 |
NL70 |
SL30 |
SL70 |
|
C7 |
2093 |
1.5 |
2.4 |
2.8 |
4.2 |
2.8 |
4.2 |
|
B6 |
1976 |
1.6 |
2.5 |
2.9 |
4.5 |
2.9 |
4.5 |
|
A6 |
1760 |
1.8 |
2.8 |
3.3 |
5.0 |
3.3 |
5.0 |
|
G6 |
1568 |
2.1 |
3.1 |
3.7 |
5.6 |
3.7 |
5.6 |
|
F6 |
1397 |
2.3 |
3.5 |
4.1 |
6.3 |
4.1 |
6.3 |
|
E6 |
1319 |
2.5 |
3.7 |
4.4 |
6.7 |
4.4 |
6.7 |
|
D6 |
1175 |
2.8 |
4.2 |
4.9 |
7.5 |
4.9 |
7.5 |
|
C6 |
1047 |
3.1 |
4.7 |
5.5 |
8.5 |
5.5 |
8.4 |
|
B5 |
988 |
3.3 |
5.0 |
5.9 |
9.0 |
5.8 |
8.9 |
|
A5 |
880 |
3.7 |
5.6 |
6.6 |
10.1 |
6.6 |
10.0 |
|
G5 |
784 |
4.1 |
6.3 |
7.4 |
11.3 |
7.4 |
11.2 |
|
F5 |
698 |
4.6 |
7.1 |
8.3 |
12.7 |
8.3 |
12.6 |
|
E5 |
659 |
4.9 |
7.5 |
8.8 |
13.4 |
8.7 |
13.4 |
|
D5 |
587 |
5.5 |
8.4 |
9.9 |
15.1 |
9.8 |
15.0 |
|
C5 |
523 |
6.2 |
9.4 |
11.1 |
16.9 |
11.0 |
16.8 |
|
B4 |
494 |
6.5 |
10.0 |
11.7 |
17.9 |
11.7 |
17.8 |
|
A4 |
440 |
7.3 |
11.2 |
13.2 |
20.1 |
13.1 |
20.0 |
|
G4 |
392 |
8.2 |
12.6 |
14.8 |
22.6 |
14.7 |
22.5 |
|
F4 |
349 |
9.3 |
14.1 |
16.6 |
25.3 |
16.5 |
25.2 |
|
E4 |
330 |
9.8 |
15.0 |
17.6 |
26.8 |
17.5 |
26.7 |
|
D4 |
294 |
11.0 |
16.8 |
19.7 |
30.1 |
19.6 |
30.0 |
|
C-m |
262 |
12.4 |
18.9 |
22.1 |
33.8 |
22.0 |
33.7 |
|
B3 |
247 |
13.1 |
20.0 |
23.5 |
35.8 |
23.4 |
35.7 |
|
A3 |
220 |
14.7 |
22.4 |
26.3 |
40.2 |
26.2 |
40.0 |
|
G3 |
196 |
16.5 |
25.2 |
29.5 |
45.1 |
29.4 |
44.9 |
|
F3 |
175 |
18.5 |
28.3 |
33.2 |
50.7 |
33.0 |
50.5 |
|
E3 |
165 |
19.6 |
30.0 |
35.1 |
53.7 |
35.0 |
53.5 |
|
D3 |
147 |
22.0 |
33.6 |
39.4 |
60.2 |
39.3 |
60.0 |
|
C3 |
131 |
24.7 |
37.7 |
44.3 |
67.6 |
44.1 |
67.3 |
|
B2 |
123 |
26.2 |
40.0 |
46.9 |
71.6 |
46.7 |
71.3 |
|
A2 |
110 |
29.4 |
44.9 |
52.6 |
80.4 |
52.4 |
80.1 |
|
G2 |
98 |
33.0 |
50.4 |
59.1 |
90.3 |
58.8 |
89.9 |
|
F2 |
87 |
37.0 |
56.6 |
66.3 |
101.3 |
66.1 |
100.9 |
|
E2 |
82 |
39.2 |
59.9 |
70.3 |
107.3 |
70.0 |
106.9 |
|
D2 |
73 |
44.0 |
67.3 |
78.9 |
120.5 |
78.6 |
120.0 |
|
C2 |
65 |
49.4 |
75.5 |
88.5 |
135.2 |
88.2 |
134.7 |
In this table,
BL30 = Length of a Brass
string at 30% Tension BL70 = Length of a
Brass string at 70% Tension
NL30 = Length of a Nylon
string at 30% Tension NL70
= Length of a Nylon string at 70% Tension
SL30 = Length of a Steel
string at 30% Tension SL70
= Length of a Steel string at 70% Tension
It is very
interesting to note that limiting lengths for steel music wire and nylon are
identical (when rounded to the nearest tenth of an inch). Remember these limits are set by two
“rules of thumb”,
that most successful string sets start with the strings at about
70% of their breaking strength in the treble end and descend to about 30% of
their breaking strength in the fourth octave where many designs start using
wound strings.
Are they really
interchangeable? Well, I have restrung a L&H folk harp (designed and initially strung with Gut)
with steel strings. To keep the tension in the same range as the gut string harp, the steel
strings had to significantly finer.
The second incarnation as a steel strung harp worked well. It did not break strings, the harp did not
implode, and the client (an ardent fan of Patrick Ball) loved the new sound.
Dubious readers
will say, “Well, OK maybe it is possible to replace nylon and gut with
finer steel strings, but this table proves that you cannot replace nylon or gut
strung harps with brass.” But does
the table really “prove” anything like that? What if we shifted the range down six notes?
|
|
|
|
||||||
|
|
|
30% |
70% |
|
|
|
30% |
70% |
|
Note |
F (Hz) |
NL30 |
NL80 |
|
Note |
F (Hz) |
BL30 |
BL70 |
|
C7 |
2093 |
2.8 |
4.2 |
|
D6 |
1175 |
2.8 |
4.2 |
|
B6 |
1976 |
2.9 |
4.5 |
|
C6 |
1047 |
3.1 |
4.7 |
|
A6 |
1760 |
3.3 |
5.0 |
|
B5 |
988 |
3.3 |
5.0 |
|
G6 |
1568 |
3.7 |
5.6 |
|
A5 |
880 |
3.7 |
5.6 |
|
F6 |
1397 |
4.1 |
6.3 |
|
G5 |
784 |
4.1 |
6.3 |
|
E6 |
1319 |
4.4 |
6.7 |
|
F5 |
698 |
4.6 |
7.1 |
|
D6 |
1175 |
4.9 |
7.5 |
|
E5 |
659 |
4.9 |
7.5 |
|
C6 |
1047 |
5.5 |
8.5 |
|
D5 |
587 |
5.5 |
8.4 |
|
B5 |
988 |
5.9 |
9.0 |
|
C5 |
523 |
6.2 |
9.4 |
|
A5 |
880 |
6.6 |
10.1 |
|
B4 |
494 |
6.5 |
10.0 |
|
G5 |
784 |
7.4 |
11.3 |
|
A4 |
440 |
7.3 |
11.2 |
|
F5 |
698 |
8.3 |
12.7 |
|
G4 |
392 |
8.2 |
12.6 |
|
E5 |
659 |
8.8 |
13.4 |
|
F4 |
349 |
9.3 |
14.1 |
|
D5 |
587 |
9.9 |
15.1 |
|
E4 |
330 |
9.8 |
15.0 |
|
C5 |
523 |
11.1 |
16.9 |
|
D4 |
294 |
11.0 |
16.8 |
|
B4 |
494 |
11.7 |
17.9 |
|
C-m |
262 |
12.4 |
18.9 |
|
A4 |
440 |
13.2 |
20.1 |
|
B3 |
247 |
13.1 |
20.0 |
|
G4 |
392 |
14.8 |
22.6 |
|
A3 |
220 |
14.7 |
22.4 |
|
F4 |
349 |
16.6 |
25.3 |
|
G3 |
196 |
16.5 |
25.2 |
|
E4 |
330 |
17.6 |
26.8 |
|
F3 |
175 |
18.5 |
28.3 |
|
D4 |
294 |
19.7 |
30.1 |
|
E3 |
165 |
19.6 |
30.0 |
|
C-m |
262 |
22.1 |
33.8 |
|
D3 |
147 |
22.0 |
33.6 |
|
B3 |
247 |
23.5 |
35.8 |
|
C3 |
131 |
24.7 |
37.7 |
|
A3 |
220 |
26.3 |
40.2 |
|
B2 |
123 |
26.2 |
40.0 |
|
G3 |
196 |
29.5 |
45.1 |
|
A2 |
110 |
29.4 |
44.9 |
|
F3 |
175 |
33.2 |
50.7 |
|
G2 |
98 |
33.0 |
50.4 |
|
E3 |
165 |
35.1 |
53.7 |
|
F2 |
87 |
37.0 |
56.6 |
|
D3 |
147 |
39.4 |
60.2 |
|
E2 |
82 |
39.2 |
59.9 |
|
C3 |
131 |
44.3 |
67.6 |
|
D2 |
73 |
44.0 |
67.3 |
|
B2 |
123 |
46.9 |
71.6 |
|
C2 |
65 |
49.4 |
75.5 |
If you scan
across the rows to the NL and BL columns you will find the length ranges are
quite close, if not identical. The
discrepancies have to do with the half steps and whole steps used in common
harp tuning scales. If one is willing to
shift the range of the instrument and
make the appropriate adjustment in string gauges, it would appear that many
harps could be strung with a broad variety of different string materials.
I will emphasize
again, before substituting different
strings materials, the harp owner needs to understand that the levers may not
work. This kind of experimentation will
void any warranty for the harp. The harp owner must be willing to bear those
risks.
Conclusions
On its own, the
Adventurous
experimenters will find
Back to the Home Page